Die Musik der Primzahlen
Primzahlen sind die "Atome" der Arithmetik - nur durch eins und sich selbst teilbar.
Gleichzeitig gehören sie zu den quälendsten Geheimnisse der Wissenschaft. 2, 3, 5, 7, 11, 13, 17,... - lässt sich voraussagen, welches die nächste Primzahl ist?
Verbirgt sich hinter dem Rhythmus ihres Auftretens vielleicht ein bestimmtes Muster? Oder gibt es gar eine Formel, mit der sich Primzahlen erzeugen lassen?
In einem ungewöhnlichen Buch wird die Geschichte der ebenso exzentrischen wie brillanten Menschen erzählt, die das Mysterium der Primzahlen zu entschleiern suchten. Der Lösung vielleicht am nächsten kam der deutsche Mathematiker Bernhard Riemann. Im Mittelpunkt seiner Überlegungen stand dabei die Idee einer Harmonie zwischen Prim- und anderen Zahlen. Nie schien man der Enthüllung des Geheimnisses der Primzahlen so nahe gewesen zu sein wie damals. Doch als Riemann starb, verbrannte eine Haushälterin alle Unterlagen, und deshalb ist die so genannte "Riemann-Hypothese" auch heute noch das große, alles überragende Rätsel der Mathematik.
"Mein Buch des Jahres" nannte Georg Steiner Sautoys großartige Erzählung von einem der großen Abenteuer des Geistes.
Marcus du Sautory, Professor für Mathematik an der Universität von Oxford und Research Fellow der Royal Society, genießt in seinem Fach hohes Ansehen. Er lebt in London, schreibt regelmäßig populärwissenschaftliche Beiträge für die "Times" und den "Guardian" und ist häufig Gast in Rundfunk und Fernsehen.
Dieses überaus zeitgemäße und spannende Buch von Marcus du Sautoy -
"Die Musik der Primzahlen" - Auf den Spuren des größten Rätsels der Mathematik
bildet in der Folge die Grundlage meiner weiteren Ausführungen.
Wer wird Millionär?
"Was ist das für eine Zahlenfolge? Okay, das können wir auch im Kopf... neunundfünfzig, einundsechzig, siebenundsechzig... einundsiebzig... Sind das nicht alles Primzahlen?" Im Kontrollraum macht sich eine gewisse Unruhe bereit. Für einen kurzen Augenblick zeigte Ellis Gesicht tiefe Erregung, die jedoch rasch wieder von einer Nüchternheit überdeckt wurde, einer Angst, sich zu vergessen oder unwissenschaftlich, dumm, zu erscheinen.
Carl Sagan, Contact
An einem heißen, schwülen Augustmorgen des Jahres 1900 hielt David Hilbert, damals Professor für Mathematik an der Universität in Göttingen, einen Vortrag an der Sorbonne in Paris. Hilbert galt bereits zu Lebzeiten als einer der größten Mathematiker seiner Zeit, und der Vorlesungssaal war bis auf den letzten Platz gefüllt. Die Nervosität in seiner Stimme war unüberhörbar, denn entgegen allen Regeln hatte Hilbert einen sehr gewagten Vortrag vorbereitet: Er wollte nicht über dinge sprechen, die bereits bewiesen waren, sondern über die noch unbekannten Dinge und über seine Vision von der Zukunft der Mathematik. "Wer von uns würde nicht gerne die Schleier lüften, unter dem die Zukunft verborgen liegt, um einen Blick zu werfen auf die bevorstehenden Fortschritte unserer Wissenschaft und in die Geheimnisse ihrer Entwicklung während der künftigen Jahrhunderte?" Und so legt Hilbert zu Beginn des neuen Jahrhundert seinen Zuhörern eine Liste von dreiundzwanzig Problemen vor, die er als richtungweisend für den Gang der Mathematik im zwanzigsten Jahrhundert einstufte.
Viele dieser Probleme fanden in den folgenden Jahrzehnten ihre Lösung, und die Entdecker dieser Lösungen gehörten einem illustren Kreis von außergewöhnlichen Mathematikern an. Hiezu zählen Kurt Gödel, Henri Poincaré und viele andere Pioniere, deren Ideen die mathematische Landschaft geprägt haben. Doch auf Hilberts Liste gab es ein besonderes Problem - das achte Problem -, von dem es den Anschein hatte, als ob es ungelöst das Jahrhundert überleben sollte: die Riemannsche Vermutung.
Von allen Problemen auf seiner Liste lag Hilbert dieses das achte Problem besonders am Herzen, das auch bis zum heutigen Tage nicht gelöst werden konnte...
Noch gut erinnerte man sich an die Begeisterung, als 1993 der englische Mathematiker Andrew Wiles einen Beweis für das letzte Fermatsche Theorem angekündigt hatte. Wiles hatte Fermats Behauptung beweisen können:
Die Gleichung xn + yn = zn hat für n größer als 2 keine ganzzahligen Lösungen.
Aber den Mathematikern war bewusst, dass ein Beweis der Riemannschen Vermutung auf die Zukunft der Mathematik weitaus größeren Einfluss haben würde als das Wissen, dass die Fermatsche Gleichung keine Lösung hat. Wie Professor Enrico Bombieri bereits mit fünfzehn Jahren festgestellt hatte, geht es bei der Riemannschen Vermutung um die grundlegendsten Objekte in der Mathematik - die Primzahlen.
Eine Primzahl ist eine ganze Zahl größer als 1, die nur durch 1 und sich selbst teilbar ist.
Jede ganze Zahl größer als 1 ist entweder eine Primzahl oder ein Produkt von Primzahlen.
Primzahlen sind gleichsam die Atome der Arithmetik. Bei den Primzahlen handelt es sich um solche unteilbare Zahlen, die sich nicht als das Produkt von zwei kleineren Zahlen schreiben lassen.
Die Zahlen 13 und 17 beispielsweise sind Primzahlen. Die Zahl 15 ist keine Primzahl, da sie sich als 3 mal 5 schreiben lässt. Wie Juwelen liegen die Primzahlen verstreut in den unendlichen Weiten des Zahlenuniversums, das von den Mathematikern über viele jahrhunderte hinweg untersucht wurde. Für Mathematiker haben sie etwas Wunderbares: 2, 3, 5, 7, 11, 13, 17, 19, 23,... - zeitlose Zahlen aus irgendeiner Welt außerhalb unserer physikalischen Realität. Sie sind das Geschenk der Natur an den Mathematiker.
Ihre Bedeutung gewinne die Primzahlen für die Mathematiker als Bausteine aller anderen Zahlen. Jede Zahl, die keine Primzahl ist, lässt sich als Produkt dieser unteilbaren Bausteine zusammensetzen. Jedes Molekül in der physikalischen Welt lässt sich aus den Atomen eines Periodensystems von chemischen Elementen zusammensetzen. Eine Liste der Primzahlen ist quasi das Periodensystem des Mathematikers. Die Primzahlen 2, 3 und 5 entsprechen im Laboratorium des Mathematikers den Elementen Wasserstoff, Helium und Lithium. Diese Bausteine besser verstehen zu können, birgt für den Mathematiker die Hoffnung, neue Wege durch die erdrückende Komplexität der Welt der Mathematik finden zu können.
Trotz ihrer scheinbaren Einfachheit und ihres grundlegenden Charakters bleiben die Primzahlen die geheimnisvollsten Objekte, die von den Mathematikern untersucht werden. Wenn es um das Auffinden von Mustern und Ordnung geht, stellen die Primzahlen eine nicht mehr zu übertreffende Herausforderung dar. Es ist unmöglich, für eine Liste von Primzahlen vorauszusagen, wann die nächste Primzahl auftauchen wird. Die Liste erscheint chaotisch, zufällig, und es gibt keinerlei Hinweise, wie man die nächste Zahl bestimmen könnte. Die Liste der Primzahlen ist der Herzschlag der Mathematik, doch dieser Puls scheint von einem stark koffeinhaltigen Cocktail angetrieben werden:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
Die ersten 100 Primzahlen
Gibt es eine Formel, mit der sich die Zahlen auf dieser Liste erzeugen lassen; irgendeine magische Vorschrift, mit der sich bestimmen lässt, was die 100. Primzahl ist?
Diese Frage hat die mathematischen Gemüter seit jeher bewegt. Doch auch nach zweitausend Jahren intensiver Suche entziehen sich die Primzahlen allen Versuchen, in ihnen irgendwelche einfachen Muster zu entdecken. Generationen von Mathematikern haben den Primzahltrommeln gelauscht: zwei Schläge, drei Schläge, fünf Schläge, sieben, elf. Und während man diese Schläge vernimmt, gewinnt man den Eindruck, irgendeinem weißen Rauschen zu lauschen, jedoch ohne innere Logik. Im Herzen der Mathematik, an der Wurzel der Ordnung, können die Mathematiker nur den Klang des Chaos vernehmen.
Wenn wir die Liste der Zahlen von 1 aufwärts durchsehen, sind Primzahlen zunächst recht häufig, werden dann aber seltener. So sind 25 % aller ganzen Zahlen unter 100, aber nur 7,9 % aller Zahlen bis 1,000.000 Primzahlen.
Da stellt sich natürlich die Frage, ob die Liste der Primzahlen irgendwann aufhört oder sich endlos fortsetzen lässt.
Euklid hat die Antwort gefunden: Es gibt unendlich viele Primzahlen. Und wie hat es das bewiesen?
Die Antwort ist: Er führte einen Beweis durch Widerspruch.
Er begann also mit der Annahme, es gebe nur endlich viele Primzahlen. In dem Fall gibt es eine größte Primzahl, die wir p nennen.
Die vollständige Liste aller Primzahlen lautet dann: 2, 3, 5, 7, 11, 13, ..., p
So weit so gut. Völlig klar, sagen Sie vielleicht. Der nächste Schritt aber war eine Eingebung.
Euklid hatte die Idee, die Zahl N = 2 x3x5x7x11 .... p +1
zu betrachten, also die Zahl, die sich ergibt, wenn man alle Primzahlen miteinander multipliziert und zu ihrem Produkt 1 addiert.
Diese Zahl N ist mit Sicherheit größer als p, und kann, da p die größte Primzahl ist, keine Primzahl sein. Es muss deshalb möglich sein, sie als Produkt von Primzahlen zu schreiben, was bedeutet, dass sie durch mindestens eine Primzahl teilbar ist.
Aber das ist sie nicht: Wenn man N durch irgendeine Primzahl aus der Liste 2, 3, 5, ..., p dividiert, bleibt immer der Rest 1.
Wir sind also auf einen Widerspruch gestoßen, der sich nur auf eine Art lösen lässt: Die ursprüngliche Annahme muss falsch sein, die Anzahl der Primzahlen kann nicht endlich sein - sie muss unendlich sein.
Es fällt den Mathematikern schwer zuzugeben, dass es möglicherweise keine Erklärung geben könnte für die Art, wie die Natur die Primzahlen ausgewählt hat. Gäbe es in der Mathematik keine Struktur, keine einfache Schönheit, lohnt es sich nicht, sie zu studieren. Dem Klang von weißem Rauschen wird man selten hingebungsvoll zuhören können. Der französische Mathematiker Henri Poincaré schrieb dazu:
"Der Wissenschaftler beschäftigt sich nicht mit der Natur, weil sie nützlich ist; er beschäftigt sich mir ihr, weil es ihm Spaß macht, und es macht ihm Spaß, weil sie schön ist. Wäre die Natur nicht schön, wäre es nicht wert, sie zu kennen, und wenn es nicht wert wäre, die Natur zu kennen, wäre das Leben nicht lebenswert."
![]()
Die Riemannsche Vermutung
Mitte des neunzehnten Jahrhunderts untersuchte Bernhard Riemann das Problem aus einer völlig neuen Perspektive und erkannte so einige der Muster, die für das Chaos der Primzahlen verantwortlich sind. Dem oberflächlichem Rauschen der Primzahlen lag tatsächlich eine subtile und unerwartete Harmonie zugrunde. Trotz diese großen Schritts blieben viele Geheimnisse dieser neuen Musik immer noch außer Hörweite. Riemann, der Richard Wagner der mathematischen Welt, ließ sich davon jedoch nicht abschrecken. Er stellte eine gewagt Vermutung über die geheimnisvolle Musik auf, die er entdeckt hatte. Dies wurde später die so genannte Riemannsche Vermutung. Wer immer auch beweisen wird, dass Riemann die Natur dieser Musik richtig eingeschätzt hatte, wird damit auch die Erklärung gefunden haben, weshalb die Primzahlen einen solch überzeugenden Eindruck von Zufälligkeit vermitteln.
Riemanns Einsicht folgte seiner Entdeckung eines mathematischen Spiegels, durch den er die Primzahlen betrachten konnte. In der Welt von Alice, der Heldin in Lewis Carrolls Erzählung Alice hinter den Spiegeln, waren rechts und links vertauscht, als Alice durch den Spiegel trat. Dem gegenüber wurde in der mathematischen Welt, die Riemann durch seinen Spiegel beobachtete, das Chaos der Primzahlen zu einem Muster, dessen Ordnung sich ein Mathematiker kaum vollkommener vorstellen konnte.
Er vermutete, dass diese Ordnung für immer erhalten blieb, wie weit auch immer man in die niemals endende Welt hinter dem Spiegel vordringen würde. Riemanns Vorhersage einer inneren Harmonie auf der anderen Seite des Spiegels würde das chaotische Verhalten der Primzahlen erklären. Die Metamorphose hinter Riemanns Spiegel, wo sich das Chaos zur Ordnung wandelt, grenzt für die meisten Mathematiker an ein Wunder. So hinterließ Riemann der mathematischen Welt eine Herausforderung:
Man beweise, dass die von ihm entdeckte Ordnung tatsächlich vorhanden sei.
Eine Lösung der Riemannschen Vermutung hätte weit reichende Auswirkungen auf mehrere andere mathematische Probleme. Die Primzahlen sind für den Mathematiker von so großer Bedeutung, dass jeder Durchbruch und jedes bessere Verständnis ihrer Natur von grundlegender Bedeutung sind. Die Riemannsche Vermutung scheint sich jedenfalls nicht umgehen zu lassen. Wie auch immer die Mathematiker sich ihren Weg durch das Gebiet der Mathematik bahnen, früher oder später scheinen alle Wege auf diese zentrale Kreuzung zu treffen.
Viele Leute haben die Riemannsche Vermutung mit der Ersteigung des Mount Everest verglichen. Je länger ein Berg unbestiegen bleibt, umso mehr drängt es uns nach seiner Eroberung. Und der Mathematiker, der den Mount Riemann als Erster erklommen haben wird, bleibt sicherlich länger in Erinnerung als Sir Edmund Hillery. Die Eroberung des Mount Everests wird nicht deshalb bestaunt, weil der Gipfel ein besonders schöner Ort wäre, sondern wegen der Herausforderungen, die mit seiner Besteigung verbunden sind. In dieser Hinsicht unterscheidet sich die Riemannsche Vermutung wesentlich von der Besteigung der welthöchsten Bergspitze. Wir alle wollen auf den Gipfel des Mount Riemann, weil uns dort ein unbeschreibliche Panorama erwartet. Die Person, die schließlich die Riemannsche Vermutung beweisen wird, füllt die Lücken in Tausenden von Theoremen, die auf der Richtigkeit der Riemannschen Vermutung beruhen. Denn viele Mathematiker mussten für Ihre Ergebnisse die Riemannsche Vermutung einfach voraussetzen.
Aus diesem Grund sprechen die Mathematiker auch häufig von der "Riemannschen Hypothese". Bei dem Wort "Hypothese" denkt man eher an eine notwendige Annahme, die man als Mathematiker zur Begründung einer Theorie macht. Demgegenüber bezeichnet "Vermutung" einfach nur eine Vorhersage, die ein Mathematiker über seine Welt trifft. Schon viele sind am Beweis des Riemannschen Problems gescheitert und haben seine Richtigkeit einfach als Arbeithypothese übernommen. Sollte also jemand die Hypothese in ein Theorem umwandeln können, wären all die unbewiesenen Ergebnisse mit einem Schlag bewiesen.
[Anmerkung: Eine mathematische Vermutung wird erst dann zu einem "Theorem", wenn ein Beweis für die Aussage dieser Vermutung vorliegt. Dieser Übergang von einer "Vermutung" oder "Hypothese" zu einem "Theorem" kennzeichnet den Reifeprozess eines mathematischen Problems. Fermat hinterließ der Mathematik einen ganzen Korb voller Vorhersagen. Es war dann den folgenden Mathematikergenerationen vorbehalten, die Fermatschen Vermutungen als richtig oder falsch zu beweisen.]
Indem sie sich auf die Riemannschen Vermutung berufen, setzen viele Mathematiker ihren Ruf auf die Hoffnung, dass eines Tages jemand die Riemannsche Vorhersage beweisen wird. Manche gehen sogar noch weiter und betrachten sie nicht nur als eine Arbeitshypothese. Für Bombieri ist es eine Glaubensfrage, dass sich die Primzahlen entsprechend der Riemannschen Vermutung verhalten. Sollte sich die Riemannsche Vermutung hingegen als falsch erweisen, würde das den ganzen Glauben in unserer Intuition in Bezug auf mathematische Zusammenhänge vollkommen zerstören. Wir Mathematiker sind mittlerweile von der Richtigkeit der Riemannschen Vermutung so überzeugt, dass alles andere ein radikales Umdenken hinsichtlich unserer Vorstellung von der mathematischen Welt erfordern würde. Insbesondere würden sich alle Ergebnisse, die wir jenseits der Mount Riemann zu sehen glauben, in Schall und Rauch auflösen.
Insbesondere könnte ein Beweis der Riemannschen Vermutung bedeuten, dass die Mathematiker ein sehr schnelles Verfahren zur Bestimmung einer Primzahl mit beliebig vielen Stellen zur Verfügung hätten. "Na und?", wird vielleicht die natürliche Reaktion des Lesers sein. Sollten Sie kein Mathematiker sein, werden Sie kaum den Eindruck haben, ein solches Ergebnis sei für ihr Leben von besonderer Bedeutung.
Primzahlen mit beispielsweise einhundert Stellen zu finden erscheint ebenso sinnlos wie das Zählen von Engeln auf einem Stecknadelkopf. Die meisten Leute würden vielleicht noch zugestehen, dass die Mathematik der Konstruktion eines Flugzeuges oder der Entwicklung der Elektrotechnik zugrunde liegt, doch nur wenige würden erwarten, dass die esoterische Welt der Primzahlen für ihr Leben irgendeine Bedeutung hat.
Sogar der G. H. Hardy war war noch 1940 dieser Meinung: "Gauß und viele weniger begabte Mathematiker konnten sich vermutlich zu Recht darüber freuen, dass es auf jeden Fall eine Wissenschaft gibt (die Zahlentheorie), die aufgrund ihrer Entfernung von den gewöhnlichen Tätigkeiten des Menschen für immer ehrlich und sauber bleiben sollte".
Doch einige jüngere Ereignisse rückten die Primzahlen ins Blickfeld der rauen und schmutzigen Welt von Wissenschaft und Finanzen. Die Zeiten, als die Primzahlen lediglich die Spielsteine in einem nutzlosen Spiel der Mathematiker waren, sind vorbei. Durch eine Entdeckung dreier Wissenschaftler - Ron Rivest, Adi Shamir und Leonard Adlemann - fanden die Primzahlen um 1970 eine weit reichend kommerzielle Anwendung. Unter der Ausnützung seiner Entdeckung von Pierre de Fermat aus dem siebzehnten Jahrhundert fanden die drei nämlich eine Möglichkeit, unsere Kreditkartennummern in den globalen elektronischen Einkaufszentren des Internets mithilfe der Primzahlen zu schützen. Als die Idee in den siebziger Jahren zum ersten Mal aufkam, konnte niemand ahnen, welche Bedeutung der elektronische Markt einmal haben würde. Heute jedoch könnte diese Geschäftsform ohne die Eigenschaften der Primzahlen nicht existieren. Jedes Mal, wenn Sie auf irgendeiner Weise eine Bestellung aufgeben, verwendet Ihr Computer ein Sicherheitssystem, das auf Primzahlen mit über hundert Dezimalstellen beruht. Nach seinen drei Entdeckern bezeichnet man dieses Verfahren als RSA. Weit über ein Million Primzahlen schützen täglich die Welt des elektronischen Handels.
Jedes über das Internet abgewickelte Geschäft beruht daher auf Primzahlen mit rund einhundert Dezimalstellen, mit deren Hilfe die Datenübertragungen sicher erfolgen können. Die zunehmende Bedeutung des Internets wird früher oder später dazu führen, dass jeder von uns eindeutig durch die ihm zugewiesenen Primzahlen identifiziert werden kann. Plötzlich gibt es also auch ein wirtschaftliches Interesse an der Frage, ob ein Beweis der Riemannschen Vermutung uns etwas über die Verteilung der Primzahlen im Zahlenuniversum sagen kann...
Ein Beweis der Riemannschen Vermutung wäre ein würdiger Abschluss für die Mathematik des 20. Jahrhunderts gewesen. Begonnen hat dieses Jahrhundert mit Hilberts Aufforderung an die Mathematiker der Welt, dieses Geheimnis zu entschlüsseln. Unter den dreiundzwanzig Problemen auf Hilberts Liste war die Riemannsche Vermutung das einzige Problem, das auch im neuen Jahrhundert noch unbezwungen sein sollte.
Am 24. Mai 2000 feierte man den 100. Geburtstag der Hilbertschen Probleme. Zu diesem Anlass versammelten sich Mathematiker und Journalisten im Collège de France in Paris, und es wurde ein neuer Satz von sieben Problemen für die Mathematik des neuen Jahrtausends verkündet. Aufgestellt hat diese Probleme eine kleine Gruppe der weltbesten Mathematiker, unter anderem Andrew Wiles und Alain Connes. Diese sieben Probleme waren gänzlich neu, mit einer Ausnahme, die schon auf Hilberts Liste stand: die Riemannsche Vermutung. Im Einklang mit den kapitalistischen Idealen, die das zwanzigste Jahrhundert geprägt hatten, erhielten diese neuen Herausforderungen eine neue besondere Würze: Die Lösung der Riemannschen Vermutung sowie der anderen sechs Probleme ist jeweils mit einem Gewinn von einer Million Dollar dotiert...
Am Tage nach der Bekanntgabe dieser Probleme war diese Website das Ziel so vieler Besucher, dass der Computer zusammenbrach.
![]()
Die Geschichte der Primzahlen - Kurzform
Das erste, wenn auch unsichere Anzeichen dafür, dass Menschen über die besonderen Eigenschaften der Primzahlen nachdachten, ist ein Knochen aus der Zeit um 6.500 v. Chr. Dieser so genannte Ishango-Knochen wurde 1960 in den Bergen von Zentralafrika entdeckt. Auf ihm sind drei Spalten von je vier Sätzen von Kerben eingeritzt. In einer der Spalten entsprechen die vier Sätze jeweils 11, 13, 17 und 19 Kerben. Dies sind sämtliche Primzahlen zwischen 10 und 20. Auch die anderen Spalten scheinen mathematischer Natur zu sein. Dieser Knochen befindet sich heute im Königlichen Institut für Naturwissenschaften in Brüssel. Es gilt jedoch als unsicher, ob er tatsächlich die ersten Versuche unserer Vorfahren darstellte, die Primzahlen zu verstehen, oder ob die Einkerbungen eine willkürliche Auswahl von Zahlen wiedergeben, die zufälligerweise Primzahlen entsprechen. Trotzdem erscheint dieser Knochen ein erstaunlicher und interessanter Hinweis auf die ersten Ausflüge in die Theorie der Primzahlen zu sein.
Manche glauben, dem Rhythmus der Primzahlentrommeln habe man zum ersten Mal in der alten chinesischen Kultur gelauscht. Die Chinesen sprachen den geraden Zahlen weibliche und den ungeraden Zahlen männliche Eigenschaften zu. Doch abgesehen von dieser einfachen Einteilung betrachteten sie solche ungeraden Zahlen, die keine Primzahlen sind - beispielsweise 15 - , als "verweichlichte" oder "unmännliche" Zahlen. Es gibt Hinweise darauf, dass sich bereits um 1000 v. Chr. ein sehr physikalisches Verständnis für die besonderen Eigenschaften der Primzahlen herausgebildet hatte. 15 Bohnen lassen sich zu einem hübschen Rechteck aus drei Reihen zu je fünf Bohnen zusammenlegen. Mit 17 Bohnen kann man jedoch nur noch ein Rechteck bilden, das aus einer einzelnen Reihe mit 17 Bohnen besteht. Für die Chinesen waren die Primzahlen so etwas wie "Macho-Zahlen", die sich jedem Versuch, sie in ein Produkt aus kleineren Zahlen zu zerlegen widersetzten.
Auch die alten Griechen schrieben den Zahlen gerne männliche oder weibliche Qualitäten zu. Im vierten Jahrhundert v. Chr. entdeckten sie jedoch auch die Kraft der Primzahlen als Bausteine für die Zahlen. Sie erkannten, dass sich jede Zahl darstellen lässt, indem man Primzahlen miteinander multipliziert.
Während die Griechen fälschlicherweise Feuer, Luft, Wasser und Erde als die Bausteine der Materie ansahen, lagen sie bei ihrer Identifikation der Atome der Arithmetik vollkommen richtig. Für viele Jahrhunderten suchten die Chemiker angestrengt nach fundamentalen Bestandteilen Ihres Gebietes, und ausgehend von den vagen Vorstellungen der Griechen gipfelten ihre Bemühungen schließlich im Periodensystem von Dmitrij Mendelejew. Damit war eine vollständige Beschreibung sämtlicher Elemente in der Chemie gefunden. Doch im Gegensatz zu dem Blitzstart der Griechen, was die Identifikation der Bausteine der Arithmetik angeht, kämpfen die Mathematiker bis heute um ein wirkliches Verständnis ihres Primzahlensystems.
Die erste Person, von der bekannt war, dass sie eine Tabelle der Primzahlen aufstellte, war der Bibliothekar des großen Forschungsinstituts der alten Griechen in Alexandria. Vergleichbar mit einem alten Mendelejew, entdeckte Eratosthenes im dritten Jahrtausend vor Christus eine verhältnismäßig einfache Methode, die Primzahlen aus einer Liste der beispielsweise ersten 1000 Zahlen herauszufinden.
Er schrieb zunächst alle Zahlen von 1 bis 1000 auf. Dann nahm er die erste Primzahl, 2, und strich jede zweite Zahl in seiner Liste durch. Da alle diese Zahlen durch 2 teilbar sind, handelt es sich nicht um Primzahlen. Dann ging er zur nächsten noch nicht durchgestrichenen Zahl, also 3. Er strich jede dritte Zahl in seiner Liste nach der 3 durch. Alle diese Zahlen sind durch 3 teilbar und somit keine Primzahlen. Und so fuhr er fort. Er nahm immer die nächste Zahl heraus, die er noch nicht durchgestrichen hatte, und strich anschließend alle anderen Zahlen, die durch diese neue Primzahl teilbar waren, heraus. Durch dieses systematische Verfahren erhielt er Primzahltabellen.
Später bezeichnete man das Verfahren als das Sieb von Eratosthenes. Jede neue Primzahl erzeugt ein "Sieb", mit dessen Hilfe Eratosthenes andere Nichtprimzahlen herausstreichen konnte. Die Größe des Siebs ändert sich bei jedem Schritt, doch wenn man schließlich bei 1000 angelangt ist, sind die Primzahlen die einzigen Zahlen, die durch alle Siebe hindurchgefallen sind...
Als Gauß noch ein Junge war, bekam er ein Buch mit einer Liste der ersten paar tausend Primzahlen, die vermutlich mithilfe dieses alten Zahlensiebs bestimmt worden waren. Für Gauß kamen diese Zahlen vollkommen zufällig daher. Hinsichtlich der Primzahlen hatte niemand auch nur die leiseste Idee, was diese Zahlen hin- und herwackeln lässt. Als Gauß seine Tabelle der Primzahlen betrachtete, fand er keine Regel, die ihm sagte, nach welchem Sprung er die nächste Primzahl finden würde.
Sollten die Mathematiker diese Zahlen einfach als naturgegeben hinnehmen wie die Sterne am Nachthimmel, ohne Sinn und Verstand? Für Gauß war eine solche Einstellung unannehmbar. Der eigentliche Grund für die Existenz eines Mathematikers ist der Wille zum Aufspüren von Mustern und Regelmäßigkeiten und zur Entdeckung und Klärung der Naturgesetze sowie die Vorhersage dessen, was als Nächstes kommt.
Die Suche nach Mustern
Was der Mathematiker in Bezug auf die Primzahlen sucht, lässt sich durch die einfache Art von Aufgabe erläutern, die uns allen von der Schule her vertraut sein durfte. Gegeben ist die Folge von Zahlen, gesucht ist die nächste Zahl. Hier drei Beispiele:
1, 3, 6, 10, 15, ...
1, 1, 2, 3, 5, 8, 13, ...
1, 2, 3, 5, 7, 11, 15, 22, 30, ...
Eine Unzahl von Fragen kommen dem Mathematiker in den Sinn, wenn er eine solche Zahlenfolge sieht. Welche Regel verbirgt sich hinter dieser Folge? Kann man die nächste Zahl in der Folge angeben? Gibt es eine Gleichung, die einem die 100. Zahl in dieser Folge erzeugt, ohne dass man die ersten 99 berechnen muss?
Die erste Zahlenfolge, 1, 3, 6, 10, 15, ... , besteht aus den so genannten Dreieckszahlen. Die zehnte Zahl in dieser Folge entspricht der Anzahl von Bohnen, die man für ein Dreieck mit zehn Reihen benötigt, wobei man mit einer Bohne in der ersten Reihe beginnt und schließlich zehn Bohnen in der letzten Reihe hat. Die N-te Dreieckszahl erhält man daher, indem man einfach die ersten N Zahlen addiert: 1 + 2 + 3 + ...+ N Möchte man die 100. Dreieckszahl berechnen, so gibt es einen langen aufwendigen Weg, mit dem man das Problem direkt angehen kann: Man addiert die ersten 100 Zahlen.
Tatsächlich war das eine Lieblingsaufgabe des Lehrers von Gauß, die er gern seinen Schülern stellte. Er wusste, dass die Schüler eine gute Weile brauchen würden, bis sie diese Aufgabe gelöst hatten. Wenn die Schüler fertig waren, mussten sie nach vorne ans Lehrerpult kommen und ihre Schiefertafeln mit den Antworten auf einen Stapel vor dem Lehrer legen. Während die anderen Schüler sich an die Arbeit machten, legte der zehn Jahre alte Gauß nach wenigen Sekunden seine Antwort auf den Pult. Der Lehrer war erbost, weil er glaubte, der junge Gauß wollte ihn ärgern. Doch als er auf die Tafel von Gauß schaute, sah er die antwort - 5050 - ohne irgendwelche Zwischenschritte in der Rechnung. Zunächst glaubte der Lehrer an irgendeinen Betrug.
Doch dann erklärte der Schüler dem Lehrer, dass man lediglich die Zahl N = 100 in der Formel 1/2 x (N + 1) x N einsetzen müsse und auf diese Weise die 100. Zahl der Folge erhält, ohne irgend eine andere Zahl der Folge vorher berechnet zu haben.
Statt das Problem mit großem Aufwand direkt anzugehen, hatte Gauß sich einen kleinen Umweg überlegt. Er dachte sich, dass man die Anzahl der Bohnen in einem Dreieck mit 100 Reihen am leichtesten erhält, wenn man ein zweites, ähnliches Dreieck von Bohnen andersherum neben das erste Dreieck legt. Nun erhält man ein Rechteck mit 101 Reihen, von denen jede 100 Bohnen enthält. Die Anzahl der Bohnen in diesem aus zwei Dreiecken zusammengesetzten Rechteck zu berechnen war leicht: Es gibt insgesamt 101 x 100 = 10.100 Bohnen. Also muss die Anzahl der Bohnen in einem Dreieck grade die Hälfte davon sein, nämlich 1/2 x 101 x 100 = 5050.

Gauß' Beweis für seine Formel der Dreieckszahlen | Die Zahl 100 hat keine besondere Bedeutung. Man kann sie durch ein beliebiges N ersetzen und erhält die Formel 1/2 x (N + 1) x N.
Statt also die vom Lehrer gestellte Aufgabe direkt anzugehen, hatte Gauß einen anderen Blickwinkel gefunden, von dem aus man die Berechnung betrachten kann. Hierin liegt auch der Grund, weshalb manche, die beispielsweise wie der junge Gauß denken, zu guten Mathematikern werden. |
Die zweite Zahlenfolge, 1, 1, 2, 3, 5, 8, 13, ..., besteht aus den so genannten Fibonacci-Zahlen. Die Regel hinter dieser Folge lautet: Man erhält die nächste Zahl, indem man die beiden vorherigen Zahlen addiert, beispielsweise 13 = 5 + 8.
Fibonacci war ein Mathematiker im 13. Jahrhundert am Hofe von Pisa. Er war auf diese Folge gestoßen, als er das Fortpflanzungsverhalten von Hasen untersuchte. Sein Modell für die Fortpflanzung der Hasen sagte für deren Vermehrung in jeder neuen Saison ein bestimmtes Muster vorher. Dieses Muster beruhte auf zwei Regeln:
Jedes erwachsene Hasenpaar zeugt in jeder Saison ein neues Hasenpaar, und jedes neue Hasenpaar benötigt eine Saison, bis es fortpflanzungsfähig ist.
Doch nicht nur in der Welt der Hasen spielen diese Zahlen eine wichtige Rolle. Die spezielle Zahlenfolge tritt in den unterschiedlichsten Zusammenhängen immer wieder auf. Die Anzahl der Blumenblätter an einer Pflanze ist häufig eine Fibonacci-Zahl, ebenso die Anzahl der Astwindungen bei einer Tanne. Auch das Wachstum einer Seemuschel zeigt im Verlauf der Zeit einen Zuwachs nach dem Muster der Fibonacci-Zahlen.
Gibt es eine Formel vergleichbar mit der Gaußschen Formel für die Dreieckszahlen, aus der man sofort die 100. Fibonacci-Zahl ablesen kann?
Zunächst hat es wieder den Anschein, als ob wir zuerst die 99 Zahlen berechnen müssen, um schließlich die 100. Zahl aus der Summe der beiden vorangehenden Zahlen zu erhalten. Kann man sich eine Formel vorstellen, in die man lediglich die Zahl 100 einsetzt und dann die 100. Fibonacci-Zahl erhält? Trotz der einfachen Regel zur Erzeugung dieser Zahlen erweist sich dieses Problem als wesentlich trickreicher.
Die Formel zur Erzeugung der Fibonacci-Zahlen beruht auf einer speziellen Zahl, die man auch den Goldenen Schnitt nennt und die mit der Ziffernfolge 1,61803 ... beginnt.
Ebenso wie die Zahl Pi (π = 3.14159265 ... auch ~ die Ludolfsche Zahl = 22/7 = das Verhältnis von Kreisumfang zu Kreisdurchmesser)
ist der Goldene Schnitt eine Zahl, deren Dezimalfolge nie endet und auch keine offensichtlichen Regelmäßigkeiten erkennen lässt. Und doch entspricht diese Zahl dem, was viele Leute über die Jahrhunderte hinweg als die "perfekte Poportion" angesehen haben.
Unteersucht man die Leinwände im Louvre oder in der Tate Gallery, so stellt man fest, dass die Künstler oft ein Rechteck gewählt haben, dessen Seitenlängen im Verhältnis 1 zu 1.61803 ... stehen.
Experimentell erweist sich auch die Größe einer Person im Verhältnis zu ihrer Höhe von den Füßen bis zum Bauchnabel als sehr nahe bei diesem Wert. Der Goldene Schnitt taucht in der Natur oft auf mysteriöse Weise auf. Trotz ihrer chaotischen Dezimalentwicklung steckt in dieser Zahl auch der Schlüssel zur Erzeugung der Fibonacci-Zahlen.
Die N-te Fibonacchi-Zahl erhält man aus einer Formel, die auf der N-ten Potenz des Goldenen Schnittes beruht.
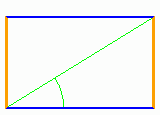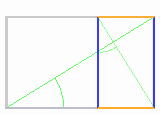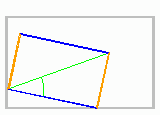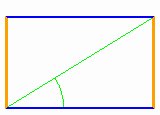 Animation Goldener Schnitt | Beschreibung
|
Die dritte Zahlenfolge, 1, 2, 3, 5, 7, 11, 15, 22, 30, ..., überlasse ich dem Leser als Herausforderung. Ich werde später noch auf sie zurückkommen. Einer der interessantesten Mathematiker des zwanzigsten Jahrhunderts - Srinivasa Ramanujan - konnte ihre Eigenschaften entschlüsseln. Dieser Mathematiker hatte eine außergewöhnliche Fähigkeit: Vor seinem inneren Auge erkannte er neue Muster und Regelmäßigkeiten, wo andere Mathematiker sich die Zähne ausgebissen hatten.
__________________________
weitere ergänzende Links aus dem iNet:
3, 6, 9 - Der versteckte Code in unserem Zahlensystem, nach Tesla - (Code)
https://www.wakenews.tv/watch.php?vid=2d4c6d8cb
https://www.wakenews.tv/watch.php?vid=18cd390e5
https://www.wakenews.tv/watch.php?vid=8a4025b78
***